UVa 10161 - Ant on a Chessboard 解题报告

原题：http://uva.onlinejudge.org/external/101/10161.html
UVa 的题目描述总是那么长，所以子勤直接跑到 nocow 去看翻译了。

棋盘上的蚂蚁（UVa 10161）这道题应该算是找规律的题吧。虽然理论上可以 1, 2, 3, 4… 地推下去，但数据范围比较大（$1 \leq N \leq 2 \times 10^9$），我觉得这样可能会超时。所以还是决定去找规律。

由于是蛇形填数，规律不容易一眼就看出来。经过近十分钟的观察和验算，我终于发现一些东西（底色高亮）：

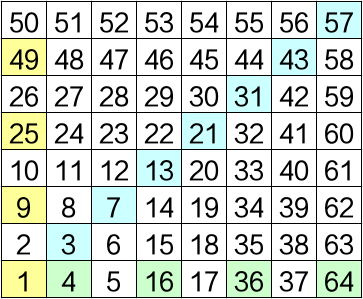
对于棋盘上的每一个数（记为 $N$），我们将它的平方根向上取整（$\lceil\sqrt{N}\rceil$，记为 Key ），可以看到：

1. 当 Key 为奇数时，$\text{Key}^2$ 在第一纵列上（黄底色）。
2. 当 Key 为偶数时，$\text{Key}^2$ 在第一橫行上（绿底色）。
3. 蓝色对角线上的数（记为 Point ）的坐标为 ( Key, Key )，值为 $\text{Key} \times (\text{Key} - 1 ) + 1$。
4. N 的橫坐标或纵坐标的其中一个一定与 Point 的相同，不同的那个可以根据 Key 的奇偶以及 N 与 Point 的差（ N - Point ，记为 c ）的正负确定方向并以 c 为步长进行偏移而得到。具体规则为：
   （1）Key 为奇数且 c 大于零时，N 的坐标为 ( Key - c, Key )；
   （2）Key 为奇数且 c 小于零是，N 的坐标为 ( Key, Key + c )；
   （3）Key 为偶数且 c 大于零时，N 的坐标为 ( Key, Key - c )；
   （4）Key 为偶数且 c 小于零是，N 的坐标为 ( Key + c, Key )。

例如要求 N 的坐标：

$N=27, \text{Key}=\lceil\sqrt{27}\rceil=6, \text{Point}=6\times(6-1)+1=31, c=27-31=-4$

由于 6 为偶数、-4 小于零，所以 27 的坐标为 (6+(-4), 6)，即 (2, 6)。

有上面的规则，写出程序就很简单了：

10161.cpp

#include <iostream>
#include <cmath>
using namespace std;
typedef long long num;
int main()
{
    num n;
    for (cin >> n; n != 0; cin >> n) {
        num key = num(ceil(sqrt(n)) + 0.5);
        num point = key * (key - 1) + 1;
        num c = n - point;
        if (key % 2) {	// key为奇数
            if (c > 0)
                cout << key - c << ' ' << key << '\n';
            else
                cout << key << ' ' << key + c << '\n';
        } else {	// key为偶数
            if (c > 0)
                cout << key << ' ' << key - c << '\n';
            else
                cout << key + c << ' ' << key << '\n';
        }
    }
    return 0;
}

成功 AC！